かけ算九九3の段−−どうしても覚えられないときに

かけ算九九が覚えられない。

でも、近いうちにかけ算九九の筆記でのテストが学校や塾である……。

困っちゃいましたね……。

最低限筆記テストをクリアするために、九九は唱えられなくても、正しい答えは出せるようにしたいはず。そんなときに役立つヒントをご紹介しています。

今回は、3の段のポイントです。

1.3の段の計算ミス

お子さんにとって、3×1や3×2、3×3の計算はさほど難しくないはずです。

しかし、指をおりをして数えるのめんどくさくなる、3×4などになると計算結果があやしくなるかもしれません。

でも、3×5ならどうでしょう。

なかなか難しいかもしれませんね。

でも、3×5が5×3と同じだというヒントを与えると、たちどころに15と正しい答えをだすことでしょう。

5という数字は子どもにイメージのしやすい数字です。 この5という数字がでてくるのは、3の段では、3×5くらいです。 なので、イメージがしやすい、3×5をうまく利用して、正しい計算結果をだせるようにしましょう。

1-1.「3×5」を中心に確認

では、3×5をうまく利用して、正しい計算結果を出すというのは、どういうことでしょう。

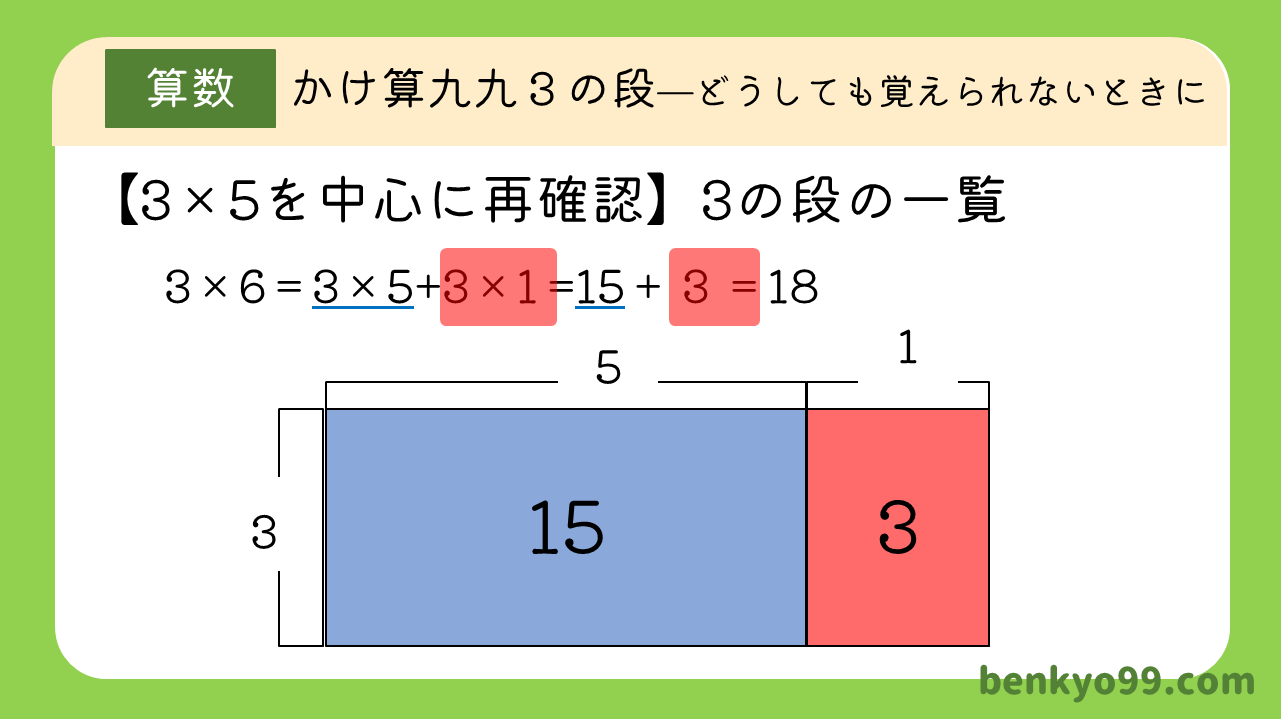
具体例があった方がわかりやすいので、「3×6」で考えましょう。

3×6の場合、3×5の計算結果に、3を足し合わせた結果が答え、つまり18になりますね。

このとき、6というのが、5＋1によって得られる数字であることをお子さんと確認して置きましょう。

数字の操作だけではお子さんには理解しづらいかもしれないので、面積図も一緒に書いて確認します。

完成する面積図は、3×5と3(×1)の二つを合体させたものになります。

3×7でも、3×8でも、同様なことをしてください。

確認するときに大切なのは、面積図を利用するということです。

これだけは絶対に省略せずに徹底してください。

実際のテストのときにも、問題用紙の隅の方に図を書けば解けるという安心感を与えることができるので、おすすめだからです。

1-2.「3×(5＋○)」の形をうまく使いこなせ

あとは、もう簡単ですね。

3×5は、5個のひとまとりがが3個あるから15個

3×6が苦手なら、3×（5+1）=(5×3)+(1×3)=15+3=15

3×7が苦手なら、3×（5+2）=(5×3)+(2×3)=15+6=15+5+1=21

3×8が苦手なら、3×（5+3）=(5×3)+(3×3)=15+9=15+5+4=24

15に、3,6,9を足し合わせた結果ですね。

3×9が苦手なら、3×（5+4）

3×4は確認していませんでしたね。

4は（5-1）の結果だから、「15から3を引けばいい」と伝えましょう。

3×4=3×(5-1)=5×3-(1×3)=15-3=12

最後に、3×9の場合。

3×（5+4）=(5×3)+(4×3)=15+12=15+10+2=27

すごく簡単ですね。

2.何も考えずにすぐ答えちゃう

どう考えても、間違いになる答えをお子さんが答えてしまう……。

でも、冷静になると、お子さんは明らかに見当違いな答えを見分けるルールをしっていないですよね。

計算ミスを減らすためにも、見当違いな答えを見つけるルール、ここでは、3の段の計算結果の法則性を見つけて見ましょう。

2-1.法則性を見つけよう

3の段の答えは、3,6,9,12,15,18,21,24,27。

法則性を見つけると言われても難しいですね。

一の位に注目すると、3→6→9→2→5→1→4→7。 十の位に注目すると、0→0→0→1→1→2→2→2。

なかなか法則性が見つけづらいですね……。

では、9の段のように、一の位と十の位を足し合わせるとどうでしょう。

3,6,9、3,6,9,3,6,9となりますね。 九九で覚える範囲だと、「3,6,9」が周期的にやってきているように見えます。 これで面白い性質を見つけられたかもしれません。

計算のコツとして「3×5」に注目しましたが、今度は「3×5」を中心にして法則を見つけてみましょう。

法則と言っても特別なものではありません。

(3×1)＋(3×9)＝30

(3×2)＋(3×8)＝30

(3×3)＋(3×7)＝30

(3×4)＋(3×6)＝30

これっていうのは、九九では覚えない、3×10の計算結果と同じですね。

他の段ではどうなっているか、時間があるときに調べて見ると面白いかもしれません。 その際、面積図を書きながら確認すると、今後の学習の内容にも接続しやすくなります。

2-2.教える立場の大人のイライラも軽減!?

こんなことをして何になると思うかもしれません。

法則性などを確認することをおすすめするのは、教える立場のお父さんやお母さんなどの大人のイライラが軽減する効果もあるかもしれないからです。

暗記物を確認するときに、お子さんが何度もくりかえし間違えると、やはりいらだってしまいますよね。暗記物の場合は、間違った答えの場合には、すぐに「違う」と伝えてしまいがちかもしれません。お子さんも何度も「違う」と言われると不機嫌になってしまいます。険悪な空気なのかで勉強するというのは、なかなかに大変なもの。

法則性を見つけるということは、かけ算九九の確認をする際に、答えがあっているかどうかをお子さん自身に確認させることができるということです。つまり、答えが間違っていたとして、ワンクッション置いて、お子さんと九九の答えの妥当性を確認ができることになります。もし、間違っていたとしても、お子さんが自身で間違いに気づけたら、「こんなのもわからんのか」という気持ちも和らぐはずです。

九九の3の段の場合は、「一の位と十の位を足し合わせると、3,6,9になる」、「30より大きい数字の答えはでてこなさそうだ」この二つの法則で確認しましょう。間違えに気づいて、暗算をする場合は、頭の中で「3×(5＋○)」の形をイメージするとミスしづらくなることでしょう。

3.おわりに

かけ算九九の3の段を覚えられないときの正しい答えを出すヒントについて紹介しました。

ひとつは、3×5に着目して面積図を使い計算を楽にするというもの。

もうひとつは、3の段の法則性に着目するというものでした。

ただ唱えて覚えた方が効率がいいと考える人もいるかもしれませんが、この方法は今後の学習の際に役立つ考え方が隠れています。どうしても覚えられないときは、長期的な視点で役に立つ考え方を教えているとつもりで、今回紹介した方法をためしてみてください。

ただ唱えるだけでは無味乾燥で嫌いというお子さんでも、自分なりに試行錯誤するのが好きな場合があるかもしれません。面積図を書いたり、法則性を見つけるという作業は、ただ唱えるよりも知的好奇心を刺激する内容なので、よりうってつけです。